As I was explaining to Gordon recently, we like to treat our classroom modules (a growing library of py files) like aquariums, small ecosystems. Then we feed their top-level denizens directly, their various functions and class constructors.Or call it "feeding the fish" maybe, drawing attention to how "top-level" really means "freely floating" in some cases, with no top-to-bottom flow of execution implied. It's a namespace, a toolbox, not a sequential story. Consider Python's math module a paradigm.
A Python module may be cast as a dynamic scratch pad, lesson plan and self-testing suite all in one, with an end user very likely another Pythonista or Pythoneer (both brands of snake charmer) and therefore having both access to, and fluency in, the module's source. There's really no need to prompt ourselves with "raw_input" as there's no "dumb user" in this picture, walled off from the code.
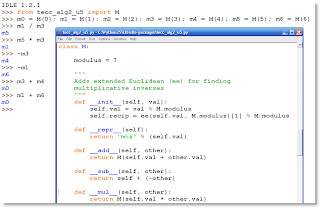
So like in the above figure: partial source for a number type M that adds, subtracts, self-negates, multiplies, divides, powers, reciprocates, always modulo some modulus, superimposed on a fragment of interactive dialog, wherein m-number objects, instances of this M class, get a workout.
A math student would typically have both windows open, switching back and forth, thereby gaining an appreciation for both the objects' encodings and their dynamic behaviors "in the field" as it were. Vectors look one way under the hood (their machinery), and another way out there in their native habitat, in action, more like spikes on a sea urchin.
We teach rational numbers, matrices, polynomials, and polyhedra the same way, as more "math objects" embedded in an extensible type system, a model that makes sense even in the context of pre-computer philosophy of mathematics discussions.
The notion of "types of object" is very ingrained in our native grammar, part of why Python "fits your brain" as they say.
