Unicode Experiments

Glenn Stockton knows a lot about the I Ching and gave me a lesson today. I'd studied The Book of Changes before, but never as deeply as Glenn has.

Now I have a new reason to revisit this ancient text: to experiment with unicode in Python.

On the Road

:: tools of the trade ::

I'm often asked what my life as a gnu math teacher is like. In some ways I'm like a journalist, with name tags like press passes, color coded to denote my rank and/or privileges, plus with these blogs in which to journal.

For example, the red tag on the right let me get up in front of the cameras in Chicago. The hand-written Portland BarCamp tag (cleverly reusable) merely announces to peer geeks that I'm interested in Python, Toons, Math e.g. my 4dstudios does mathcasting around Python quite a bit.

I don't actually encourage stuffing two CubeIts! in your carry-on, as the 24 MITEs apiece are highly magnetized, might mess with your other media.

:: close up ::

And speaking of "on the road," my uncle Bill Lightfoot was by today, sans the red Aztek, which he'd exchanged for a newer white one.

Happy Birthday Matt, great being included in your family, since age five or six as the neighborhood newbie. Wonderful seeing all those brothers and sisters again, plus spouses and offspring.

Gnu Math Chatter

Per my Chicago Pycon talk, an early bridge twixt lexical math type expressions and graphical sphere packing ala the IVM (CCP, FCC) are the figurate and polyhedral number sequences, developed minus any foreground coordinate system apparatus, although you need something under the hood in support of the ray tracer (a mechanical device).

This focus on geometric growth (gnomon studies) is prominent in late 20th century geometry: The Book of Numbers by Conway and Guy, Encyclopedia of Integer Sequences by Sloane et al (AT&T), Gnomon by Midhat Gazale, and of course Cuisenaire bricks ala Caleb Gattegno (more about linear color coded distances and the various time serialized entrainings thereof).

Coxeter was leading this charge in many dimensions with polyhedral numbers -- made sense Bucky would see the connection twixt his own deliberately remote vocab and this soon to be mainstream stuff.

Pascal's Triangle and Tetrahedron form a Grand Central here, where these many threads converge / diverge. Python insinuates some generators at this point, syntax that has already spread to the latest JavaScript, along with list comprehensions, in turn credited to Haskell no? The languages all swap DNA with wild abandon -- actually in tightly controlled fashion, but still not predictably.

Pascal's Triangle and Fibonacci Numbers are part of what go out preloaded on XOs, those "little green monsters" (Shrek colored) showing up in places like Peru, Uruguay... Alabama, any number of privileged homes in North America. The application is called Pippy and provides early exposure to Python.

Math Objects

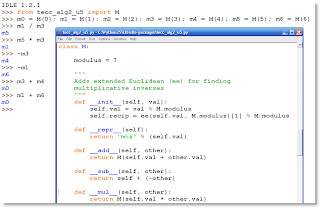As I was explaining to Gordon recently, we like to treat our classroom modules (a growing library of py files) like aquariums, small ecosystems. Then we feed their top-level denizens directly, their various functions and class constructors.

Or call it "feeding the fish" maybe, drawing attention to how "top-level" really means "freely floating" in some cases, with no top-to-bottom flow of execution implied. It's a namespace, a toolbox, not a sequential story. Consider Python's math module a paradigm.

A Python module may be cast as a dynamic scratch pad, lesson plan and self-testing suite all in one, with an end user very likely another Pythonista or Pythoneer (both brands of snake charmer) and therefore having both access to, and fluency in, the module's source. There's really no need to prompt ourselves with "raw_input" as there's no "dumb user" in this picture, walled off from the code.

So like in the above figure: partial source for a number type M that adds, subtracts, self-negates, multiplies, divides, powers, reciprocates, always modulo some modulus, superimposed on a fragment of interactive dialog, wherein m-number objects, instances of this M class, get a workout.

A math student would typically have both windows open, switching back and forth, thereby gaining an appreciation for both the objects' encodings and their dynamic behaviors "in the field" as it were. Vectors look one way under the hood (their machinery), and another way out there in their native habitat, in action, more like spikes on a sea urchin.

We teach rational numbers, matrices, polynomials, and polyhedra the same way, as more "math objects" embedded in an extensible type system, a model that makes sense even in the context of pre-computer philosophy of mathematics discussions.

The notion of "types of object" is very ingrained in our native grammar, part of why Python "fits your brain" as they say.

Crossing Paths

We took in Bodies today, now at the Carnegie Science Center in Pittsburgh, PA.

I'm getting to know this traveling exhibition quite well, having first encountered it in London, traveling solo, then again in Seattle with Tara and Dawn.

Alexia, Pat and Lil had not seen it before.

Body Worlds 3, which came through Portland, is a separate production.

This morning I posted more of my usual to math-teach @ Math Forum, from Indiana, PA.

I'm glad we included a Garmin StreetPilot with the Alamo rental car. She -- female voice, we nicknamed her Bessie -- got us all the way from Chicago, no other maps needed.

Fractions R Us

:: congrats to anna ::

[first posted to Math Forum, earlier today (typos fixed for this version, code colorized)]

I'm noticing with our novel approach to teaching fractions, that we're discounting the importance of the LCM in connection with adding them. The reason for that is our use of Euclid's Algorithm for the GCD upon instantiation, meaning when we create a fraction object, we automatically convert to the canonical delegate in each equivalence class, namely that for which the numerator and denominator are relatively prime.

The background context is "building fractions" (yes, this is constructionism) from the ground up, in some computer language facilitating operator overloading. That's right, we're doing some programming as a part of our standard mathematics curriculum, what of it? TIs have been programmable for years, and we've heard no one fussing ("more features!" has always been the battle cry, no?).

As I've posted about numerous times here (math-teach), irrespective of whether programming's involved, it's interesting to see if a curriculum dodges Euclid's Method for finding the GCD, escaping into "factor trees" (which I have nothing against -- very important for teaching the meaning of the Fundamental Theorem of Arithmetic).

I'd call that a kind of litmus test, to see if your proposal meets minimum standards -- let's apply it to the states first and foremost, see which state legislatures are being lobbied intelligently, vs. getting fed a lot of mumbo jumbo. Good project for a PhD candidate.

So how do we add fractions then? Of course the old fashioned way: a/b + c/d == (a/b)(d/d) + (c/d)(b/b) == (ad + cb)/bd as justified by using multiplicative identity, other axioms (I'm sure Paul could help out here).

Then you get gcd((ad + cb), bd)), call it thegcd (could be 1), so your new (reduced) numerator, denominator (p,q) become p/thegcd, q/thegcd (multiplying by x/x is to multiply by 1, the multiplicative identity -- this came up earlier, in justifying (a/b)==(a/b)(d/d).

How does this look in actual Python? Here's a fraction class (rational number class) developed to the point of enabling its instances (p/q) to multiply and add (p,q integers, q <> 0). Click for larger views.



Kirby

PPUG 2008.3.11

Our core presentation was on Mocker, a code testing tool.

I stayed late seeking to help a guy with some confusing code.

In the background, I empathized with a Python teacher told to keep certain core concepts off limits in the name of keeping the course introductory.

And yet it's harder to master Python if you have to bleep over the part about its being an object oriented language. What does that even mean? My advice: start early with objects.

My hope is our brand of college prep math, laced with computer programming, will result in much stronger computing skills among new recruits.

Mortgage Mess

Omitted from most journalistic accounts of the mortgage meltdown, is the fact that some well off North Americans no longer dream of McMansions, but have their hearts set on something from the pages of Ecotrust, a very high tech fishing village, complete with broadband and real fishing.

So yes, post Depression Era bulwarks against conflicts of interest, enormous temptations to cheat, were gradually eroded away, like dikes in New Orleans, leaving USAers with few protections against predators (Congress was in on the deal). That's certainly part of it, and we've had no shortage of accounts taking this line.

But since the 1930s and before, this culture has nursed utopian visions in which we get off the grid, or at least have more freedom. Mobile home and RV subcultures, plus the usual yachting crowd, have prototyped the lifestyle. What's missing is much investment by aerospace companies, the ongoing status quo so long as cruise missiles appear the safer bet, Airstream an exception.

So another part of the story is simply not wanting to admit failure. The Vietnam generation wasted helicopters on military instead of civilian enterprising, and now we're all paying, with squalid living standards, stuck with housing designs from the dark ages.

More Technoinvective

Fixed a typo, hyperlinks added.

Haim:

> Now, think of the math curriculum from arithmetic
> to the calculus as a closed system.

Now that's pretty clear. And I tend to agree with "closed" as in "not very open to sensory input" e.g. any proverbial "writing on the wall."

My own view of the curriculum, even K-12, is of a creature much more amoeboid and morphic, able to resequence and reshape far more radically than your theory'd permit.

I'd go with energy conservation though, as in: the average individual spends x calories over y hours towards developing her or his numeracy skills, whatever those may be in some culture. We don't easily squeeze more juice from the same finite time budget (and lets not forget sports practice, also very important).

"Capable of radical overhaul" is actually a good feature, because our world is fast changing, and freezing the numeracy content to a snapshot of what it once was, would make no sense at all. Also, it's a character trait of many USAers to welcome change. Oregon, home of the Trailblazers, is imbued with such a pioneering spirit.

However, within that context, of a liberal arts space, there are, I'd agree, these relatively rigid (calcified) "dead horse" shapes, of which I think the traditional late 1900s USA pre-calc-to-calc sequence is an excellent example.

Kirby

Wanderers 2008.3.4

Although I've resigned from any management responsibilities with Portland Wanderers, I still attend the neighborhood meetings at Linus Pauling House.

Tonight I showed up with my projector and flipped through a few items, including a preview of my Chicago Pycon talk.

Also, since Barry was telling Peace Corps stories from Brazil, focusing on Manaus and "rubber barons" enamored of opera, I couldn't resist seeking Fitzcarraldo links on Youtube and dredging up the Klaus Kinski vs. Jason Robards clip -- takes me back.

Bill has been writing a port scanner in assembler and had himself talking to a USB port at home. But on his Dell Inspiron, the same ports appear inert.

Aldona is a Lithuanian name. Her mom didn't learn English until later, as that Shenandoah mining community had its Lithuanian section, where one could get by in that language. Good seeing Steve again.

Bridging the Gap

Xrefs:
Reviewing some Theory... (Math Forum essay)
Pascal's Tetrahedron
Binomial Theorem
Focal Points
Boosting Bandwidth