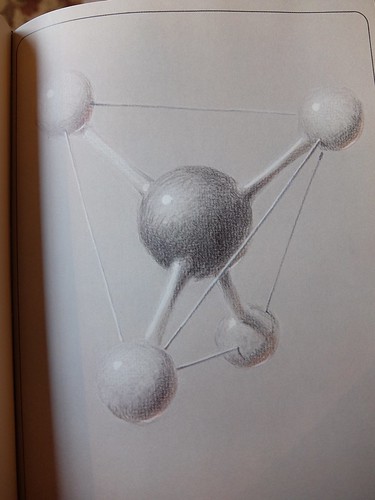
Some teachers stress about curriculum segments on polyhedrons, such as the Platonic Five, as where and when will these prove useful? Do we really have the luxury of "going there" with so much of STEM still waiting?
I don't think the arrangement of space into coherent, oft repeating, patterns is a waste of time. Glenn's recent find at Good Will reminds me: Linus Pauling merged spatial geometry with chemistry in ways we'll never forget.
On the same topic, congratulations to Julian for that write-up in the Portland Tribune. He's the sculptor behind Alpha Helix next to the Linus Pauling House on Hawthorne, directly across from Third Eye.
I'm at the other end of the spectrum, stressed about the exclusion of polys, and curating textbook titles for our World Game Museum.
Secondary school textbooks that skimped on polyhedrons, the tetrahedron especially, while purporting to be STEM-worthy might get some critical write-ups in our retrospective.
Why the tetrahedron in particular? Of the Platonic Five, or of any, it's topologically the simplest, called the simplex for that reason. No arrangement of fewer edges joined at corners has a spatial inside. A triangle fences a field but doesn't define a cage (enclosure).
We're in the realm of Euler's Law for Polyhedrons, likewise Descarte's Deficit of 720 degrees. The numberphiles on Youtube will explain what those mean. Such pillar concepts mark out a common core of cultural literacy. A common core minus V + F == E + 2 would be exhibit-worthy for its grave deficiency.
If you're a teacher in a Freedom School or one of those, and have the luxury of escaping from the "down the drain" vortex of the left-behind curricula, you'll have access to the resources you need to keep it real. Help your colleagues who aren't so lucky?
I don't think the arrangement of space into coherent, oft repeating, patterns is a waste of time. Glenn's recent find at Good Will reminds me: Linus Pauling merged spatial geometry with chemistry in ways we'll never forget.
On the same topic, congratulations to Julian for that write-up in the Portland Tribune. He's the sculptor behind Alpha Helix next to the Linus Pauling House on Hawthorne, directly across from Third Eye.
I'm at the other end of the spectrum, stressed about the exclusion of polys, and curating textbook titles for our World Game Museum.
Secondary school textbooks that skimped on polyhedrons, the tetrahedron especially, while purporting to be STEM-worthy might get some critical write-ups in our retrospective.
Why the tetrahedron in particular? Of the Platonic Five, or of any, it's topologically the simplest, called the simplex for that reason. No arrangement of fewer edges joined at corners has a spatial inside. A triangle fences a field but doesn't define a cage (enclosure).
We're in the realm of Euler's Law for Polyhedrons, likewise Descarte's Deficit of 720 degrees. The numberphiles on Youtube will explain what those mean. Such pillar concepts mark out a common core of cultural literacy. A common core minus V + F == E + 2 would be exhibit-worthy for its grave deficiency.
If you're a teacher in a Freedom School or one of those, and have the luxury of escaping from the "down the drain" vortex of the left-behind curricula, you'll have access to the resources you need to keep it real. Help your colleagues who aren't so lucky?