I was just posting to Facebook that "bridging the gap" would be a great first tourist stop in the mathemagical theme park (we use Python __magic__ sometimes).
Here is where we familiarize ourselves with the concept of Zonohedra.
A zonohedron has faces with opposite-edges-parallel (picture a stop sign), minimally rhombi, as well as opposite parallel faces, like a cube has, or a rhombic dodecahedron.
The rhombic triacontahedron is likewise a zonohedron and our "gap" inheres here, between two of them.
Consider two RTs (thirty diamond faces each) of almost exactly the same volume, but the one is a little smaller, making for two sets of faces, one set slightly within the other.
Along each radial, from the body center, two diamond faced centers occur, towards the tip. There's a tiny gap between the two.
Here's the ratio we go by: the RT inside, the slightly smaller one, has a volume of exactly 5, relative to the reference tetrahedron of edges 2R.
The ball of radius R very slightly protrudes, at each face center, a small hump, a pitcher's mound. The apex of each hump marks the center of a 5+ volumed RT's face.
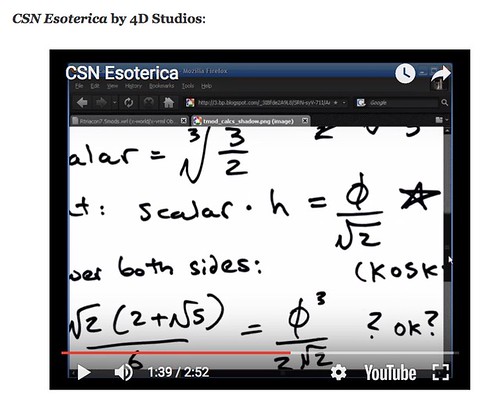
Each RT has a "nice" property: a volume of precisely 5, a radius of precisely R. The latter, scaled up by Φ, becomes yet another RT of volume 20 * √(9/8).
When we scale the smaller volume five RT up by 1.5 or 3/2 as a scale factor, its volume turns into 7.5 (red), and its radius into Φ/√2. It now shares a set of vertexes with the volume 6 RD (yellow).
The new face radius, of the 7.5 volumed RT, will be the 3rd root of 3/2 times whatever it was before (call it h), since to boost a volume by 3/2, the edges need to expand by the 3rd root of that number, or about 1.14471424255333.
The resulting face center to body center radius (believe it or not): Φ/√2 where √ and sqrt mean the same thing, arithmetically.
In other words, the original h, for which the RT has a volume of exactly 5, is Φ/√2 multiplied by the reciprocal of the 3rd root of 3/2, or about 0.99948333226234344.
Another tad-bigger RT, has a radius of R precisely, just a tad larger than the volume 5 RT's of radius 0.9995, weighing in at about 5.00775803133283.
The tag-bigger RT's volume is granule greater than 5, of necessity, but look at how tiny the gap in radius: 0.000516667737 is pretty small, compared to 1 R, the reference length.
That's why we might pay you to pay some mind to this little difference. Without concerted attention, it might be overlooked. Attention means concentration means doing work (measured in iota perhaps).
Let's take stock of what juggling balls we get in the air with this exhibit:
- 2nd and 3rd roots and powers
- the golden ratio Φ
- the power rule (relating linear to areal to volumetric growth)
- two spheres (and a thin wall between them)
- a pair of RTs (tiny difference in radius, volumes 5 & 5+)
- an RT of volume 7.5 sharing vertexes with the RD of volume 6
- an RT of ~21.21 embedding the Jitterbug icosahedron (as long diagonals)
- five concentric zonohedra (six counting the cube of volume 3)...
- one of which is the the space-filling RD of volume 6
- the concept of tetravolumes
- T & E modules (RT)
- A & B modules (RD)
- alternative powering models
- scaling by Φ
What schools have a mandate to teach this stuff? Paw through Youtube? I'm finding more researchers getting a clue.
We might call this exhibit Prying Open Synergetics as we're managing to suck some sense out of a hairline fracture that came to light only after Dr. Fuller already had put some years of concentration into his newly emerging discipline.