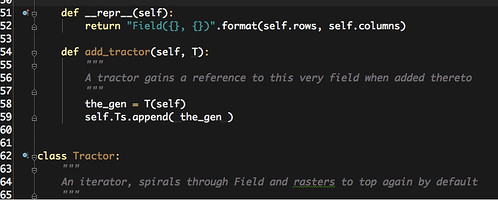
... the Dell in the Farmer. Lets think of a farmer riding a tractor, the tractor in a field. Yes, the farmer is in the field, but then so has the farmer internalized the field, a mental field. People do that with fields. In the computer language I'm learning, Python, the method for adding a Tractor to a field is a time to give the farmer, the self of the Tractor, a handle on the Field.
the self of "this Field" is provided to the "self" of the added Tractor
One may view that in source code at GitHub, where Lesson1.py defines the Field and Tractor, along with a subclass of Tractor for writing in the field.
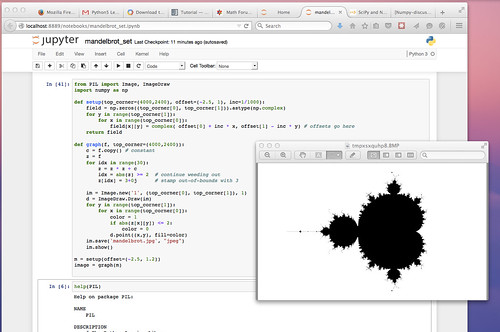
Then Lesson2.py defines another subclass of Tractor, the CropCircleTractor, that appropriately plows or plants a Mandelbrot in its Field. The output is just a text file, ASCII art, whereas in future Lessons one might use PIL, or POV-Ray, or VRML or even Visual Python.
The Field is an XY layer, a grid of cells each addressed by two numbers, a familiar tool. Piling up these layers, 3D Printer style, would be a way to encompass Volume which contains shapes we might address in various ways, perhaps with XYZ coordinates, adding Quadrays as a less familiar tool for contrast. The Mandelbrot might become a Mandelbulb instead.
The Tractor comes with a TV-like raster motion. A real tractor would turn around and come back the other way, but this one works more like a spiral, as if the end of a row connected to the beginning of the next at the other side of the field.
Then, having traversed the very last row and coming to the end, the Tractor magically reappears at the start again, to begin its trek all over. What we lose in freedom, we gain in the simplicity of the code. Provided the Tractor has enough fuel (there's a fuel_level), every cell will get visited within a circular topology.
Another subclass yet, of which I've already done some versions, plays a Game of Life using rule-governed cellular automata.
Might we alter the Field class to consist of hexagons instead? Games of Life may be played that way too, and are, quite a lot.
Could our Volume be as if filled with rhombic dodecahedra, perhaps using Quadrays again?
These vistas stretch out before us, which speaks well for the simple ladder that got us up this high, where we get lots of overview.