Valentine's Day 2006

cute

I'll be using the same home-brewed Pygame-based presentation manager code I wrote for OSCON 2005 to drive my presentation to Winterhaven's sixth graders on Thursday morning (soon after I teach my Python class). We've booked the auditorium -- this'll be a good test of my projector's luminosity.

I'll be taking them through Polyhedra 101: some classification schemes (e.g. Platonic and Archimedean), and a nesting scheme (which implies some relative sizing or scaling).

Of course I'm focusing on Fuller's nesting scheme, because he's the positive futurist and great American writer they need to learn about. Plus his way of doing polyhedra is pretty memorable and compact, so we'd likely cover it even if he weren't a Medal of Freedom winner.

RBF

Other MoF winners include: thespians Carol Burnnet, Bill Cosby and Andy Griffith, boxer Muhammed Ali, spy chief George Tenet, Fed chairman Alan Greenspan, TV show hosts Fred Rogers and Julia Child, management guru Peter Drucker, First Lady Nancy Reagan, soldiers Colin Powell, Tommy Franks, Wesley Clark and William Crowe, Pope John Paul II, and Gordon Moore of Moore's Law fame -- quite the mixed bag (wouldn't you say?) and that's only a small sampling of the list.

The CCP lattice sets the stage. Around each CCP sphere: a space-filling rhombic dodecahedron. Its long diagonals: an octahedron. Its short diagonals: a cube. Inscribed within the cube: two tetrahedra as alternate sets of face diagonals. Relative volumes: 6 : 4 : 3 : 1.

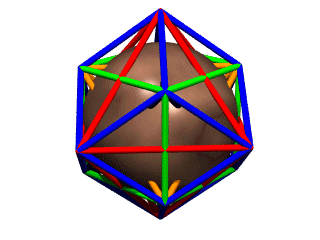
nesting scheme

Twelve CCP spheres around the nuclear sphere define the cuboctahedron, of relative volume 20. Packing outward in successive layers, we get 12, 42, 92, 162... spheres, always in a cuboctahedral conformation.

CCP

My intent is to get down to the A and B module dissections; all of the aforementioned polys may be assembled from these two tetrahedral slivers, each of relative volume 1/24. As a hands-on activity, students will fold left and right handed A modules from the plane nets I'll hand out, then assemble regular tetrahedra therefrom.

We bridge to five-fold rotationally symmetric territory by crossing the "Jitterbug Bridge" -- a visual transformation taking the cuboctahedron into an icosahedron, which, along with its dual, the pentagonal dodecahedron, complete the Platonics.

This is stuff every elementary schooler should get briefed on -- or their American heritage is being denied them [visual: waving flag; sound track: patriotic fife and drum].

Today (Valentine's Day, 2006) even some top lawyers in Washington DC are ignorant of these basic math facts, which really hurts their credibility and effectiveness as potential USA OS operatives in my book, as this means they have a poor grasp of their own American History.